What the Data Says: A Literary Analysis
- ctpartin
- Apr 16, 2019
- 7 min read
So what exactly does this data analysis approach tell us about The Sonnets? What literary information can we gleam, what structure can we uncover? In order to answer this question and present the literary insights gained from the project, I have broken up this up into four sections, each one detailing a different aspect of the structure of The Sonnets: Cataloging, Creating a Map, Outliers, Cycles.
Cataloging
In this first section I will discuss and present the full cataloging of the repeated words and phrases from The Sonnets that I looked at. This is also a good place to talk about an important aspect of this project, and that is the fallibility of the human mind. I cannot claim with 100% certainty that this is a full and proper cataloging of all repetitions in The Sonnets. And if anything I claim that this is not a full cataloging. But I can claim that this cataloging covers the most important and most frequent and then some, hopefully being enough data to properly support the claims that I will later make.
Here is the catalog in its entirety, 76 words and phrases repeated over 79 sonnets:

As it is impossible to read the catalog from just this picture, the excel file containing all the data will be available to download on the resources page to view in further detail
The rows of the catalog represent the different repeated elements, while the columns represent the individual sonnets. A green cell means that sonnet contains that element, while a blank cell the opposite. From the catalog we can already see some basic patterns about how The Sonnets is constructed. It is not hard to notice that the density of green cells increases as we go further to the right along the catalog. This show us that the number of repeated elements grows in frequency as we progress along the book, explaining that sense of familiarity as one approaches the end of the book. We can also see, interestingly enough, the sonnets that don’t contain any repetitions in them at all, such as “Poems in a Traditional Manner” and “Mess Occupations”. But clearly, deciphering all the patterns here with the human eye is nigh impossible. That is why we turn to mathematics and computer science to do some of the pattern recognition for us. You can read more about how the process works in the other post, but here we will merely be discussing the results of the calculations and what it means for making sense of the structure of The Sonnets.
Creating a Map
One of the most interesting and useful applications of our mathematical approach is to be able to visualize the structure of The Sonnets. You can read in the post about the mathematics how we acquire these visualizations, but for the purposes of the literary analysis, it is helpful to just view the results:
If you want to explore these more, you can click the links on the resources page to find an interactive version of both visualizations where you will be able to see which sonnet map to which point. Now the obvious question to ask is what these visualizations are supposed to represent in regards to the sonnets. The important thing to keep in mind is that in both representations, distance is the key. What the axes of the plots are don’t matter (this is explained better in the math post), but rather how far apart the points are for each sonnet. Sonnets that are closer to each other on the plots are sonnets that are in a sense “more similar” in respect to sharing more of the repeated elements. There are various techniques to capturing this notion of sameness, thus resulting in the two different visualizations you see here. The main difference between the two is how they capture similarity versus differences between sonnets. The plot on the left is better at capturing difference in the sonnets, while the plot on the right is better at showing similarities. We will use the data from both of these soon to explore specific properties of certain sonnets that they reveal, but first we will look at a purely visual aspect of both of them that highlights some of the structure in The Sonnets.
We will examine some visual structure by drawing a line chronologically through the data points. Meaning that it will connect points that follow each other sequentially in the book.
Doing this for both plots gives us these new plots:
Now at first these seem practically impossible to glimpse any information from, as they are quite busy graphics. In order to try and understand a little bit better what is going on, I highlighted the first line segment green and the last one red, so you can get some understanding of the path of the line. What this graphic does show us though is an amazing visual of how interwoven The Sonnets really is. Most of the time the sonnets do not sequentially relate, rather they relate to poems that are not sequentially close at all. Though we can find pockets of sequential poems that are also closely related in terms of repetition. For example, on the plot on the right, there is a group of sonnets in the upper right hand corner that are closely related in terms of repetition but also in terms of being sequentially close to one another, these are the sonnets: LIII, LV, and LVI. We will discuss more examples of these groupings later when we talk about cycles, but these graphics provide an excellent visual for how The Sonnets is sequentially constructed. It brings to light how much the book connects itself throughout, not just building up sequentially, but rather connecting all sonnets together in a web of repetition and structure.
Outliers
An important part of any data analysis is finding which points lie outside of most of the data, in other words, which points are outliers. For us this amounts to finding the sonnets which seem disconnected from most of the other ones. Which ones does the data show us stand out on their own from the rest of the book? The way that we find these is discussed in greater detail in the post on the mathematics behind this analysis, but the idea is that using the representation that is better at characterizing differences in the sonnets, we will find which ones are further than the majority. Using an algorithm we were able to assign a numerical value describing how much of an outlier an individual sonnet is, essentially describing what fraction of the sonnets this particular sonnet is disconnected from. Here is what the algorithm gives us:
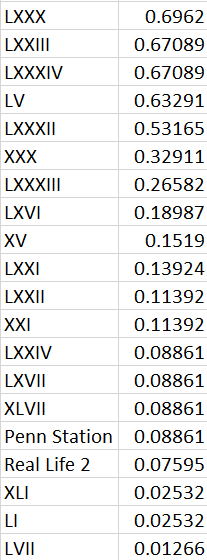
From this data we are able to find sonnets that are not as connected to the rest of the book as others are. Meaning that there are few other poems that share most of the repetitions that these do. It is important to note that these sonnets being outliers does not imply they do not contain repeated words and phrases, rather that the specific selection of repetitions they do contain are an uncommon one in the book. We can see that based on the data, there are sonnets close to each other sequentially towards the end that seem to stand out amongst most of the book. This is something that isn't apparent just looking at repetitions, as they do include repetitions, its just the ones they share might not closely align with a majority of the sonnets. From this data it is also interesting to note that besides this clump of sonnets at the end, most of the other sonnets are not that disconnected from the rest. The outlier number drops dramatically from 0.53 to 0.32 after the 5th outlier, and continues to steadily to drop until it reaches 0 after there are 20 sonnets which are somewhat considered outliers. What this means is that most of the book is highly interconnected, with many sonnets sharing lots of repeated phrases. There is high variety and high density in the number of repetitions, leaving very little sonnets stranded out in the open. Almost all sonnets have some connection to another, and most of them have many connections to many other sonnets.
This data also provides a selection of unique sonnets to possibly be looked at on their own. One can see if there are aspects of their literary construction that makes them stand out as an outlier besides their disconnectedness in repetitions.
Cycles
The last and one of the most intriguing aspects of the structure of The Sonnets that we are going to focus on is the idea of cycles. Now intuitively what I mean by cycles is small groupings of sonnets that are highly related to each other. I use the term cycle merely in regards to how they are found (which can be found in the post on the mathematics behind all of this), but essentially they are sub-groupings of sonnets that are highly related in terms of repetition. Due to the construction of the book, there are lots of different possibilities of cycles, and the algorithm I use to find them allows us to find a large selection of them, as well as an arbitrary size of them. Due to the almost endless possibilities, I will provide and look at only a small sample selection here, but the code is available on the resources page for anybody to play around with and generate new cycles to be explored. Here is just a sample of some possible cycles that exist within The Sonnets:
Length 2: LXXVIII, XXXIII
XXVII, V
XLIV, LXXXIV
LXXVIII, LXXVII
V, XXXI
Length 3: V, XXXI, XIII
LXVIII, I, XVIII
LXXVII, LXXVIII, XXXVI
LXXVIII, LXVIII, V
XXXVI, III, XXXIII
Length 4: XLI, LV, XXIX, LXXVIII
LXXVII, LXXVIII, LXXV, V
XVII, IV, XLI, XXI
LXXVIII, LXXVII, XXXIII, XXXVI
I tried to generate longer cycles, but the issue is that as the cycle length increases, the amount of computing power needed to find accurate, meaningful, and useful cycles increases exponentially. There are some ways the algorithm could be improved in terms of time efficiency and finding more meaningful cycles, which I will discuss in a post about how this project could be expanded on going forward. The most important part of these cycles is that they give us small clusters of sonnets to focus our attention on, looking at why it be that this small group of sonnets is considered so closely related.
An interesting thing to note about the cycles is that one sonnet may find itself in multiple cycles. While this may not be too surprising, it does lead to a general observation about how interconnected The Sonnets truly is. One sonnet can find itself being connected to a multitude of others, and in various ways. The way that the repetitions are structured allow there to be an almost endless way to group and study the various sonnets. There isn't necessarily one specific structure or one proper grouping, instead there exists an uncountable array of structures, each representing a different aspect of The Sonnets. It seems to turn out that asking the question what is THE structure of The Sonnets is not the correct question to ask. Instead the question to ask is what are the different structures created by Berrigan's purposeful and intricate use of repetition, and what do each of these unique structures say about the book as whole? This idea of cycles and the algorithm to find them does just this, and will hopefully prove to be a useful tool for future scholars of the book.











Comments